==Test== Functions & Plugins

Citation and Reference

Here is a example of citing a reference [1]. Here is a multiple citation[2, 3].

Two citations with space in between [2, 3]. Three citations with no space in between [1, 2, 3].

Footnote

• Here’s a short footnote with number tag.¹
  • The markdown syntax is [^1]
  • The footnote syntax is [^1]: This is a short footnote.
• Here’s a longer one with a custom tag.²
  • E.g. [^longnote]
  • E.g. [^longnote]: This is a longer footnote with paragraphs, and code.

Figure and Caption

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nullam elementum, ipsum non finibus sodales, tellus sapien pulvinar enim, at sollicitudin felis dui ut lectus. Important content could be emphasised using **bold** or __bold__ text. Duis venenatis, lectus a efficitur laoreet, metus eros suscipit mi, nec posuere lorem diam eget eros. Donec porttitor enim eros, et luctus elit gravida at. Praesent venenatis ultrices consequat.

Figure 1.  Training steps of ChatGPT: Transformer, Pre-traing, Supervised Fine-tuning (SFT), and Reinforcement Learning from Human Feedback (RLHF)

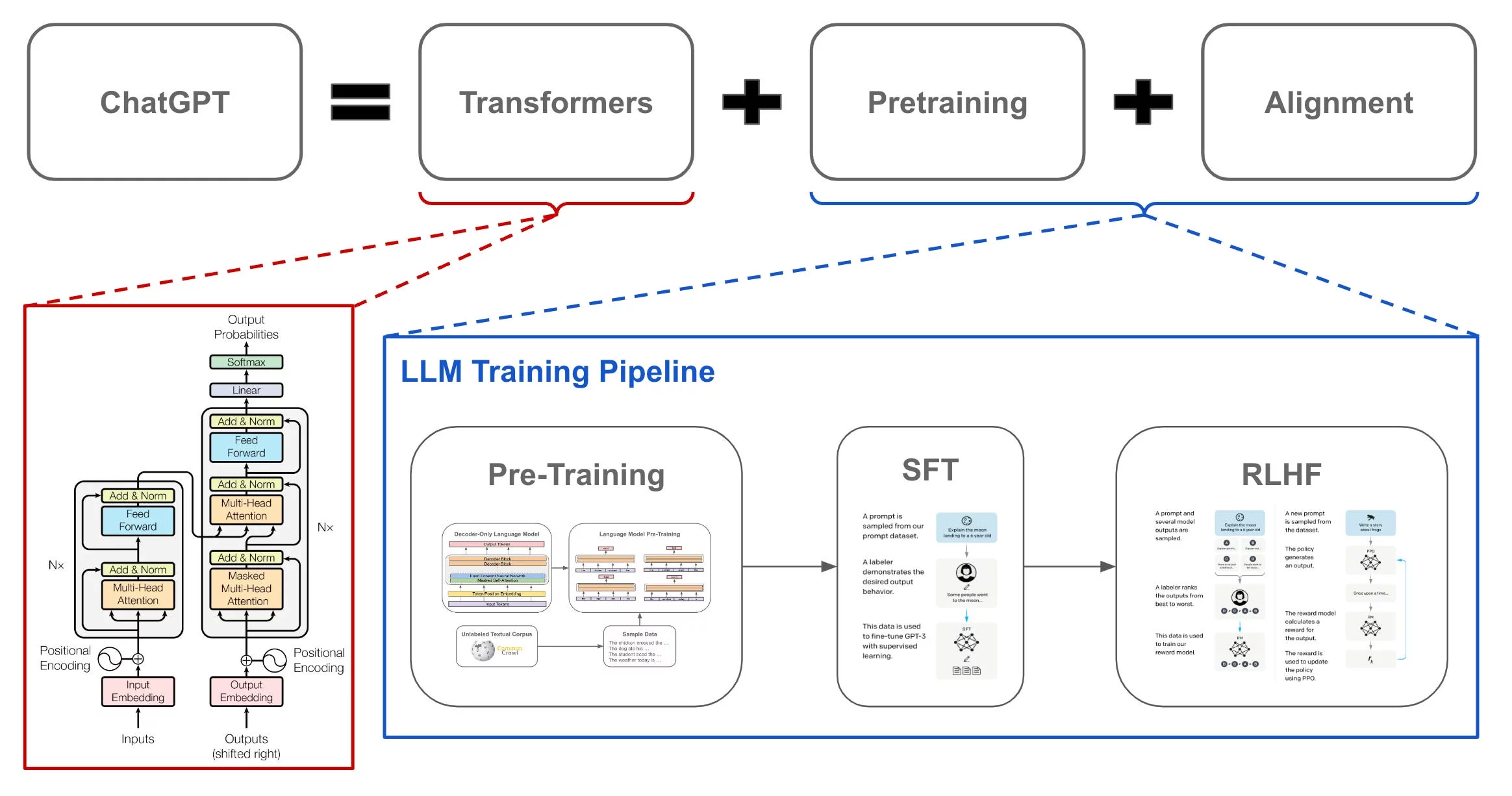
Integer mattis, lacus vel porta tristique, velit felis faucibus velit, non fermentum urna risus sit amet justo. Nunc tempus, augue vel imperdiet viverra, sapien lacus facilisis dui, ac malesuada magna eros quis arcu. Aliquam tempor purus nec est eleifend tincidunt.

Figure 2.  Example of terminal

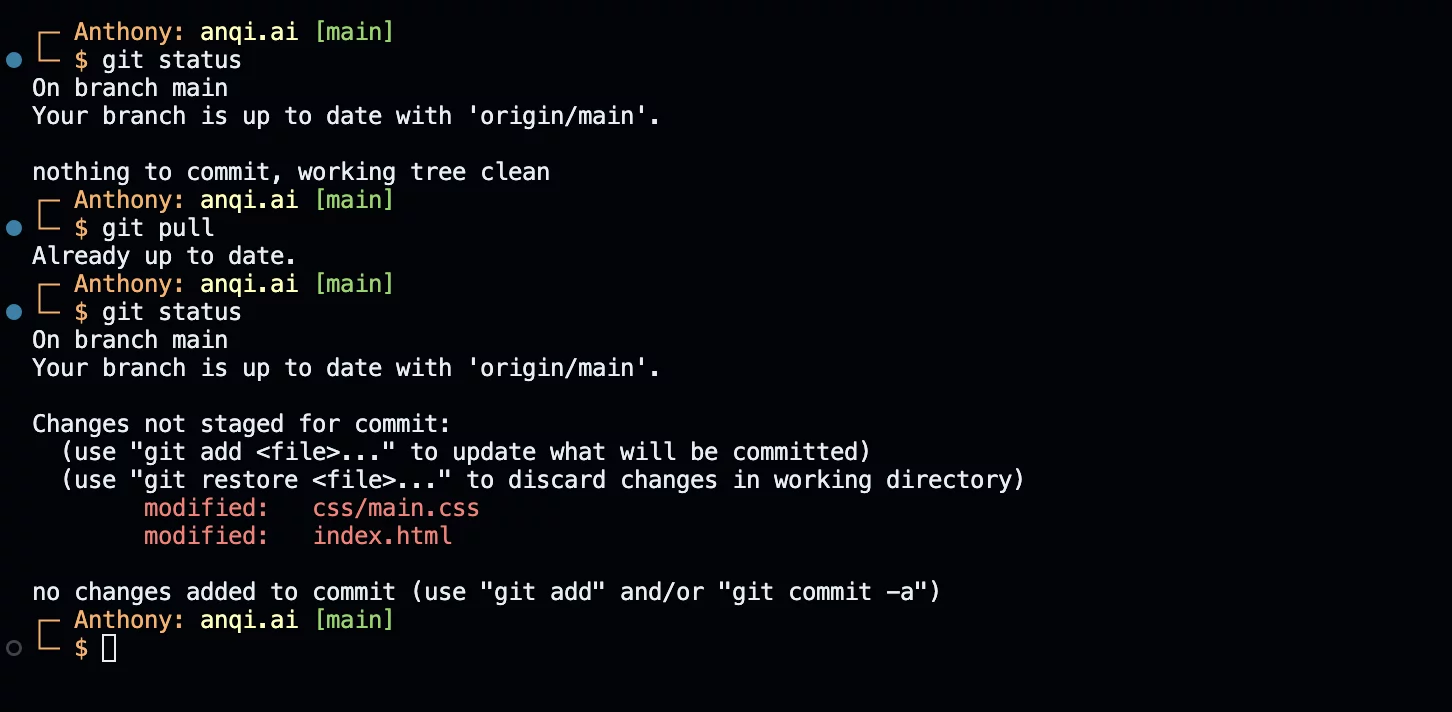
Sed vel turpis congue ipsum pulvinar hendrerit sit amet nec est. Aliquam et elit eu ante suscipit finibus non quis dui. Mauris turpis tellus, convallis quis libero et, vestibulum viverra lacus.

Figure 3.  Decoder component of Transformer architecture

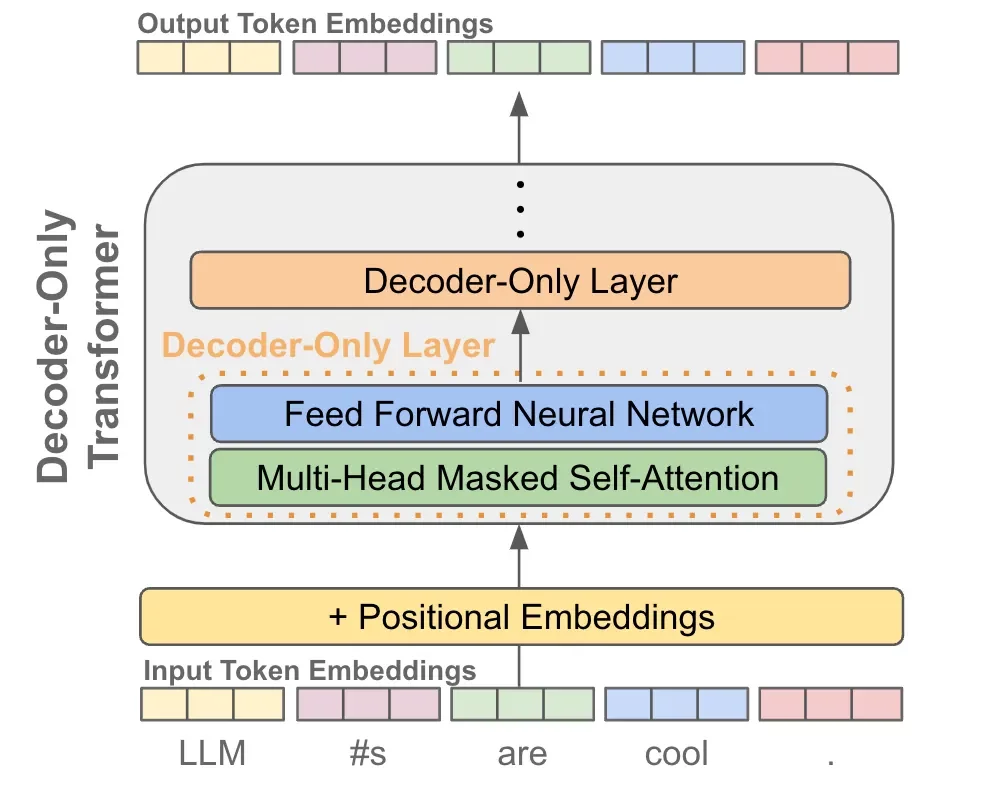
LaTeX Formula

Here is the LaTeX formula for the cross-entropy loss, which is commonly used in machine learning, particularly for classification tasks:

For a binary classification problem, the cross-entropy loss $ L $ is defined as:

$L = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right] \tag{1}$

Where:

• $ N $ is the number of samples
• $ y_i $ is the true label (0 or 1) for the $ i $-th sample
• $ p_i $ is the predicted probability of the $ i $-th sample belonging to class 1

For a multi-class classification problem, the cross-entropy loss $ L $ is defined as:

$L = - \frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{i,c} \log(p_{i,c}) \tag{2}$

Where:

• $ N $ is the number of samples
• $ C $ is the number of classes
• $ y_{i,c} $ is a binary indicator (0 or 1) if class label $ c $ is the correct classification for sample $ i $
• $ p_{i,c} $ is the predicted probability of sample $ i $ being in class $ c $

You can use these formulas in your LaTeX document as follows:

% Binary cross-entropy loss
L = - \frac{1}{N} \sum_{i=1}^{N} \left[ y_i \log(p_i) + (1 - y_i) \log(1 - p_i) \right]

% Multi-class cross-entropy loss
L = - \frac{1}{N} \sum_{i=1}^{N} \sum_{c=1}^{C} y_{i,c} \log(p_{i,c})

Conclusion

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Etiam eros quam, vulputate sed lacus in, sodales sagittis arcu. Maecenas sagittis euismod ligula eu venenatis. Mauris eget consequat tortor. In eu ultricies dui. Cras elementum, leo eu rutrum rutrum, mi neque malesuada sem, non fermentum est nunc sed mauris. Maecenas id.